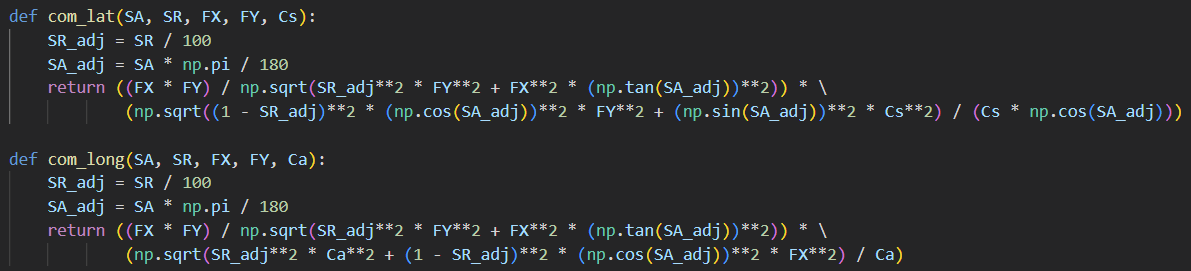
In the previous section, I made independent fits for lateral and longitudinal tire forces. However, lat and long are functions of each other, so our independent models aren't exactly accurate. To account for this difference we need a combined loading model, and I've opted for the Nicolas-Comstock model. For this model, we take our existing lateral and longitudinal fits and pass them through a set of corrections (note that you also need to implement very heavy zero protection to avoid division by zero errors. I won't detail those here, but they caused most of the issues I had with implementing this model). I've included snippets of the corrections below:
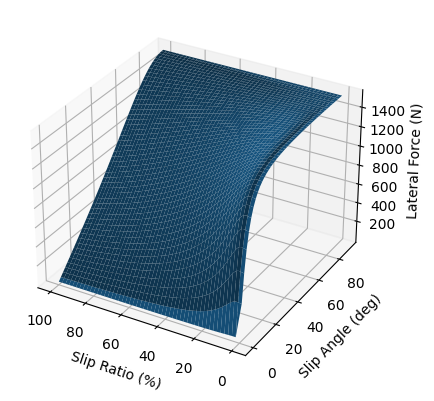
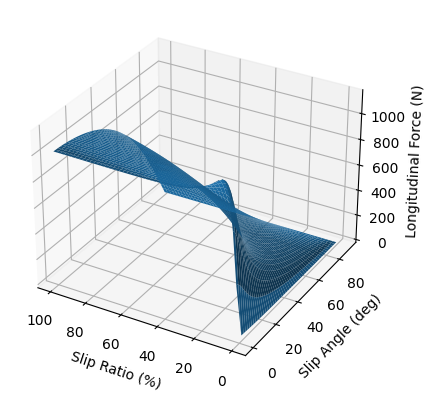
We can then use the functions above to iterate over the entire domain of adjusted lateral and longitudinal forces. I've included the adjusted lateral fit on the left and the adjusted longitudinal fit on the right. Also note that the lateral fit didn't take slip ratio before, and the longitudinal force didn't take slip angle before. Now, both fits are a function of both slip angle and slip ratio (although these are the main parameters we care for in this study, other factors such as normal force, incliniation angle, tire pressure, tire temperature, etc have effects on the pacejka fits we based these combined models on).
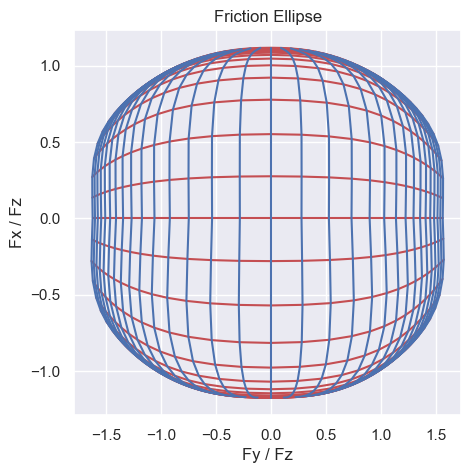
We can then use these fits to create a tire ellipse and fully visualize our model. On here we can plot lateral force, longitudinal force, and isolines of both slip angle and slip ratio. I've plotted this below, and it let's us see whether we follow expected behavior (easiest way to check for zero protection and edge cases). I've also normalized the lateral (Fy) and longitudinal (Fx) forces by dividing by normal force (Fz):