
For the purpose of tire characterization, companies take a tire and run it on a test jig, recording parameters pertinent to the tire's state and performance. The purpose of tire fitting is to make predictions based on the set of data provided from testing.
One of the most common methods for tire characterization is using the method described by Hans Pacejka. In this model, you use the Pacejka Magic Formula and solve for a set of coefficients. After this, you can plot over the entire domain of the Magic Formula and pure your lateral force, longitudinal force, and aligning moment for a set of inputs. I've included an image of the general model for lateral fits below:
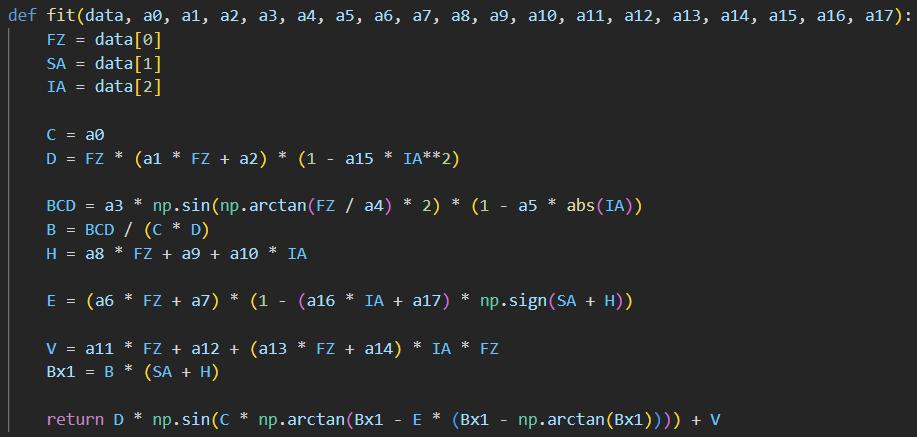
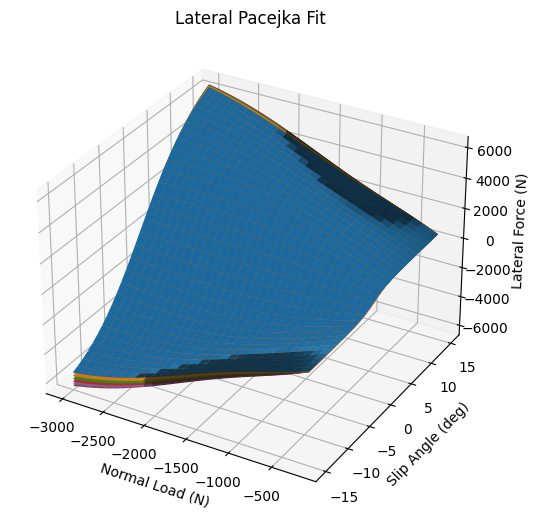
In this function, we take normal force, slip angle, inclination angle, and Pacejka coefficients as inputs. We then return the lateral force. With this setup, we can vary the Pacejka coefficients until our fit matches the set of data points provided from tire testing. I've plotted the entire domain for multiple inclination angles (each inclination angle adds a unique surface) for a set of generated coefficients.
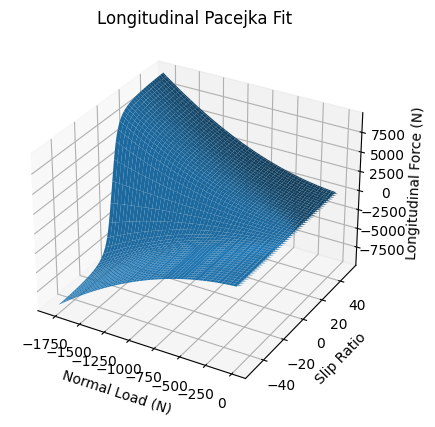
This process also works for longitudinal fitting (the coefficients change for this case). I've included a sample longitudinal fit below:
The most difficult part of the fitting process is solving for the best Pacejka coefficients. I originally tried using Scipy surface fitting, but this becomes less effective as you add more coefficients. I ended up using a cost function and basin hopping algorithm. The cost function summed the difference between the fit and its corresponding data point. The basin hopping algorithm allowed me to approximate a global minimum from a collection of local minima. This allowed me to bypass the issues from typical gradient descent methods, and I arrived at a set of reasonable coefficients after strategically varying the initial guess for each coefficient.